Blog Pensi

No post do nosso especial #PensinaAprovação de hoje, trouxemos o conteúdo e as dicas referentes à disciplina Matemática. Nossa equipe de professores experts preparou uma série de vídeos para que você consiga mandar muito bem e alcançar os melhores resultados. Se quiser preparar aquela pipoca para lanchar enquanto estuda, é uma ótima pedida. Ah! Lembre-se: você pode acessar todos os outros conteúdos do especial #PensinaAprovação, é só clicar no link do seu interesse abaixo.

• #PensinaAprovação – Especial Redação

• #PensinaAprovação – Especial História

• #PensinaAprovação – Especial Geografia

• #PensinaAprovação – Especial Filosofia 

• #PensinaAprovação – Especial Sociologia

• #PensinaAprovação – Especial Biologia

• #PensinaAprovação – Especial Química

• #PensinaAprovação – Especial Física

Vamos às dicas dos conteúdos mais cobrados em Matemática? Então continue lendo 😉

1. Dica da professora Ana Eliza – Visualização

2. Dica do professor Yuri Politano – Razões e proporções

3. Dica do professor Anderson Machado – Arranjo e combinação

4. Dica do professor Eduardo Avellar – Porcentagem

5. Dica da professora Fernanda Erculano – Função

6. Dica do professor Sérgio Gomes – Equação da Circunferência

Ultimamente  os conceitos básicos de geometria analítica são bastante recorrentes nas provas do ENEM e o enfoque costuma ser no conceito de ponto, reta e circunferência.

Os problemas que envolvem o conceito de equação da circunferência são normalmente os problemas que  apresentam os maiores níveis de dificuldades para os candidatos.

Então, vamos recordar!?

A geometria analítica fornece uma ferramenta algébrica (analítica) para o estudo de informações  geométricas.

Uma circunferência é formada por um conjunto de pontos que apresentam uma distância fixa (raio) em relação a um centro definido.  Quando  a mesma está locada no plano cartesiano podemos facilmente verificar a equação da circunferência.

Vamos lá!

Agora, genericamente, considerando C (a,b) o centro, r o raio e P (x,y) um ponto da circunferência, temos:

OBS.: No caso particular de o centro da circunferência estar na origem, ou seja, a=b=0, a equação da circunferência é :

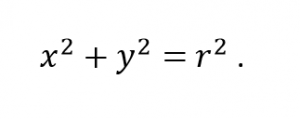
Ao desenvolvermos a equação da circunferência   obtemos o que denominamos de equação geral  da circunferência abaixo:

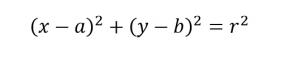
Obtemos o que denominamos de equação geral  da circunferência:

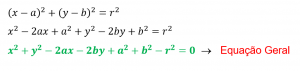
E aí? Anotou tudo? Em 2021 queremos ver você se tornando um universitário e vamos com tudo te ajudar a alcançar esse sonho!